Compact Finite Difference Schemes
Per-Olof Persson
persson@berkeley.edu
Math 228B Numerical Solutions of Differential Equations
Approximation of First Derivative
Consider a uniformly spaced mesh \(x_i=hi\) with given function values \(f_i=f(x_i)\). Seek approximations to the first derivative at the nodes \(f'_i=f'(x_i)\) of the form \[\begin{aligned} \beta f'_{i-2} &+ \alpha f'_{i-1} + f'_i + \alpha f'_{i+1} + \beta f'_{i+2} \\ = &c \frac{f_{i+3}-f_{i-3}}{6h} + b \frac{f_{i+2}-f_{i-2}}{4h} + a \frac{f_{i+1}-f_{i-1}}{2h} \end{aligned}\]
Match Taylor series coefficients for order conditions: \[\begin{aligned} a+b+c &= 1+2\alpha+2\beta & &\text{(2nd order)} \\ a+2^2b+3^2c &= 2\frac{3!}{2!}(\alpha+2^2\beta) & &\text{(4th order)} \\ a+2^4b+3^4c &= 2\frac{5!}{4!}(\alpha+2^4\beta) & &\text{(6th order)} \\ a+2^6b+3^6c &= 2\frac{7!}{6!}(\alpha+2^6\beta) & &\text{(8th order)} \\ a+2^8b+3^8c &= 2\frac{9!}{8!}(\alpha+2^8\beta) & &\text{(10th order)} \end{aligned}\]
Tridiagonal Schemes
If \(\beta=0\) and \(\alpha\) nonzero, tridiagonal systems need to be solved to obtain the derivative approximations
If in addition \(c=0\), a one-parameter (\(\alpha\)) family of 4th order tridiagonal schemes is obtained: \[\begin{aligned} \beta=0,\quad a=\frac23 (\alpha+2),\quad b=\frac13 (4\alpha-1),\quad c=0 \end{aligned}\]
Special cases:
\(\alpha=0\) gives the standard 4th order central difference scheme,
\(\alpha=1/4\) gives the classical Padé scheme.
\(\alpha=1/3\) gives a 6th order accurate scheme: \[\begin{aligned} \alpha=\frac13,\quad \beta=0,\quad a=\frac{14}{9},\quad b=\frac19\quad c=0 \end{aligned}\]
Tridiagonal Schemes
If \(\beta=0\) and \(c\ne 0\), a one-parameter (\(\alpha\)) family of 6th order tridiagonal schemes is obtained: \[\begin{aligned} \hspace{-3mm} \beta=0,\quad a=\frac16 (\alpha+9),\quad b=\frac{1}{15} (32\alpha-9),\quad c=\frac{1}{10}(-3\alpha+1) \end{aligned}\]
Special cases:
\(\alpha=3/8\) gives an 8th order accurate scheme: \[\begin{aligned} \beta=0,\quad a=\frac{25}{16},\quad b=\frac{1}{5},\quad c=-\frac{1}{80} \end{aligned}\]
Pendadiagonal Schemes
If \(\beta\ne 0\) and \(c = 0\), a one-parameter (\(\alpha\)) family of 6th order pentadiagonal schemes is obtained: \[\begin{aligned} \hspace{-6mm} \beta=\frac{1}{12}(-1+3\alpha),\quad a=\frac29 (8-3\alpha), \quad b=\frac{1}{18} (-17+57\alpha),\quad c=0 \end{aligned}\] which becomes an 8th order scheme if \(\alpha=4/9\): \[\begin{aligned} \alpha=\frac49,\quad \beta=\frac{1}{36}, \quad a=\frac{40}{27}, \quad b=\frac{25}{54}, \quad c=0 \end{aligned}\]
If \(\beta\ne 0\) and \(c \ne 0\), a one-parameter (\(\alpha\)) family of 8th order pentadiagonal schemes is obtained: \[\begin{aligned} \hspace{-16mm} \beta=\frac{1}{20}(-3+8\alpha),\ a=\frac16 (12-7\alpha), \ b=\frac{1}{150} (568\alpha-183),\ c=\frac{1}{50}(9\alpha-4) \end{aligned}\] which becomes a 10th order scheme if \(\alpha=1/2\): \[\begin{aligned} \alpha=\frac12,\quad \beta=\frac{1}{20}, \quad a=\frac{17}{12}, \quad b=\frac{101}{150}, \quad c=\frac{1}{100} \end{aligned}\]
Approximation of Second Derivative
Seek approximations to the second derivative at the nodes \(f''_i=f''(x_i)\) of the form \[\begin{aligned} \hspace{-7mm} \beta f''_{i-2} &+ \alpha f''_{i-1} + f''_i + \alpha f''_{i+1} + \beta f''_{i+2} \\ =\, &c \frac{f_{i+3}-2f_i+f_{i-3}}{9h^2} + b \frac{f_{i+2}-2f_i+f_{i-2}}{4h^2} + a \frac{f_{i+1}-2f_i+f_{i-1}}{h^2} \end{aligned}\]
Match Taylor series coefficients for order conditions: \[\begin{aligned} a+b+c &= 1+2\alpha+2\beta & &\text{(2nd order)} \\ a+2^2b+3^2c &= 2\frac{4!}{2!}(\alpha+2^2\beta) & &\text{(4th order)} \\ a+2^4b+3^4c &= 2\frac{6!}{4!}(\alpha+2^4\beta) & &\text{(6th order)} \\ a+2^6b+3^6c &= 2\frac{8!}{6!}(\alpha+2^6\beta) & &\text{(8th order)} \\ a+2^8b+3^8c &= 2\frac{10!}{8!}(\alpha+2^8\beta) & &\text{(10th order)} \end{aligned}\]
Tridiagonal Schemes
If \(\beta=0\) and \(c=0\), a one-parameter (\(\alpha\)) family of 4th order tridiagonal schemes is obtained: \[\begin{aligned} \beta=0, \quad c=0,\quad a=\frac43(1-\alpha),\quad b=\frac13 (-1+10\alpha) \end{aligned}\]
Special cases:
\(\alpha=0\) gives the standard 4th order central difference scheme,
\(\alpha=1/10\) gives the classical Padé scheme.
\(\alpha=2/11\) gives a 6th order accurate scheme: \[\begin{aligned} \alpha=\frac{2}{11},\quad \beta=0,\quad a=\frac{12}{11},\quad b=\frac{3}{11},\quad c=0 \end{aligned}\]
Similarly to before, higher order and pentadiagonal schemes can be derived
Fourier Analysis
Assume periodic domain \([0,L]\) with \(f_1=f_{N+1}\) and \(h=L/N\)
Decompose variables into fourier coefficients \[\begin{aligned} f(x) = \sum_{k=-N/2}^{n=N/2} \hat{f}_k \exp \left( \frac{2\pi i kx}{L} \right) \end{aligned}\]
Introduced scaled wavenumber \(w=2\pi k h / L = 2\pi k / N\) in the domain \([0,\pi]\), and the scaled coordinate \(s=x/h\), giving Fourier modes \(\exp(iws)\)
The exact first derivative generates Fourier coefficients \(\hat{f}'_k = iw \hat{f}_k\)
Compare with the coefficients \((\hat{f}'_k)_{fd}=iw'\hat{f}_k\) obtained from the differencing scheme
Modified wavenumber, first derivatives
The first derivative approximations: \[\begin{aligned} \beta f'_{i-2} &+ \alpha f'_{i-1} + f'_i + \alpha f'_{i+1} + \beta f'_{i+2} \\ = &c \frac{f_{i+3}-f_{i-3}}{6h} + b \frac{f_{i+2}-f_{i-2}}{4h} + a \frac{f_{i+1}-f_{i-1}}{2h} \end{aligned}\] corresponds to \[\begin{aligned} w'(w) = \frac{a\sin(w) + (b/2)\sin(2w) + (c/3)\sin(3w)} {1+2\alpha\cos(w)+2\beta\cos(2w)} \end{aligned}\]
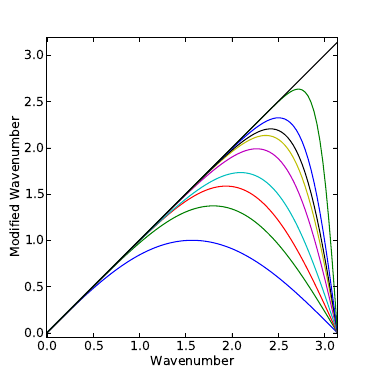
From bottom to top: 2nd order central, 4th order central, 4th order central, standard Padé, 6th order tridiagonal, 8th order tridiagonal, 8th order pentadiagonal, 10th order pentadiagonal, spectral-like, exact differentiation
Modified wavenumber, second derivatives
The exact second derivative generates Fourier coefficients \(\hat{f}''_k = -w^2\hat{f}_k\)
Compare with the coefficients \((\hat{f}''_k)_{fd}=-w''\hat{f}_k\) obtained from the differencing scheme
The second derivative approximations: \[\begin{aligned} \hspace{-8mm} \beta f''_{i-2} &+ \alpha f''_{i-1} + f''_i + \alpha f''_{i+1} + \beta f''_{i+2} \\ =\, &c \frac{f_{i+3}-2f_i+f_{i-3}}{9h^2} + b \frac{f_{i+2}-2f_i+f_{i-2}}{4h^2} + a \frac{f_{i+1}-2f_i+f_{i-1}}{h^2} \end{aligned}\] corresponds to \[\begin{aligned} \hspace{-8mm} w''(w) = \frac{2a(1-\cos(w))+(b/2)(1-\cos(2w))+(2c/9)(1-\cos(3w))} {1+2\alpha\cos(w)+2\beta\cos(2w)} \end{aligned}\]
Non-Periodic Boundaries
Find first derivative at the boundary \(i=1\) by one-sided approximation: \[\begin{aligned} f'_1+\alpha f'_2 = \frac{1}{h}(af_1 + bf_2 + cf_3 + df_4) \end{aligned}\]
2nd order accuracy requires \[\begin{aligned} a=-\frac{3+\alpha+2d}{2},\quad b=2+3d,\quad c=-\frac{1-\alpha+6d}{2} \end{aligned}\]
Third and fourth order schemes can also be derived
Harder to study using Fourier analysis
Filtering
Find filtered values \(\hat{f}_i\) from an approximation \[\begin{aligned} \beta \hat{f}_{i-2} &+ \alpha \hat{f}_{i-1} + \hat{f}_i + \alpha \hat{f}_{i+1} + \beta \hat{f}_{i+2} \\ = & af_i + \frac{d}{2} (f_{i+3} + f_{i-3}) + \frac{c}{2} (f_{i+2}+f_{i-2}) +\frac{b}{2}(f_{i+1}+f_{i-1}) \end{aligned}\] with transfer function \[\begin{aligned} T(w) = \frac{a+b\cos(w)+c\cos(2w)+d\cos(3w)} {1+2\alpha\cos(w)+2\beta\cos(2w)} \end{aligned}\]
Impose \(T(\pi)=0\), and possibly higher order derivatives
Match Taylor series coefficients for high formal accuracy
Filtering
Set \(\beta=0\) for tridiagonal system, use one free parameter \(-0.5<\alpha\le 0.5\):
\[\begin{aligned} &(F2)\quad a =\frac12 + \alpha,\quad b=\frac12+\alpha \\ &(F4)\quad a =\frac58 + \frac{3\alpha}{4},\quad b=\frac12 +\alpha \,\quad c=-\frac18 + \frac{\alpha}{4} \\ &(F6)\quad a =\frac{11}{16} + \frac{5\alpha}{8},\quad b=\frac{15}{32} + \frac{17\alpha}{16},\quad c=-\frac{3}{16}+\frac{3\alpha}{8},\quad d=\frac{1}{32}-\frac{\alpha}{16} \end{aligned}\]
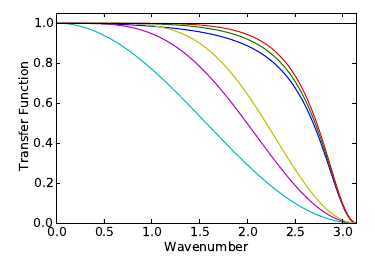
From left to right:
\((F2)\ \alpha=0\), \((F4)\ \alpha=0\), \((F6)\ \alpha=0\),
\((F2)\ \alpha=0.45\), \((F4)\ \alpha=0.45\),
\((F6)\ \alpha=0.45\),