The Level Set Method – Lecture Notes
Per-Olof Persson
persson@berkeley.edu
Evolving Curves and Surfaces
Evolving boundaries or interfaces are part of many problems in science and engineering. In 1988, James A. Sethian and Stanley Osher proposed to represent these boundaries implicitly and model their propagation using appropriate partial differential equations. The boundary is given by level sets of a function \(\phi(\boldsymbol{x})\), and they named their technique the Level Set Method. These notes give a short introduction to the method, and for more details we refer to the books by Sethian and Osher , as well as their original paper .
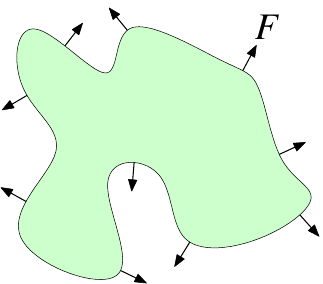
Consider a boundary curve in two dimensions or a surface in three dimensions, see Figure 1. We are given a velocity field \(\boldsymbol{v}\), which in general depends on space, time, properties of the boundary (such as the normal direction and the curvature), as well as an indirect dependence from physical simulations using the boundary shape. To goal is to accurately model the evolution of the boundary under the velocities \(\boldsymbol{v}\). In many cases we are only interested in the motion normal to the interface. We can then use a (scalar) speed function \(F\), and let the velocities be given by \(\boldsymbol{v}=F\boldsymbol{n}\), where \(\boldsymbol{n}\) is the normal direction.
Explicit Techniques
A simple approach to model the boundary motion is to represent it explicitly, for example (in two dimensions) by nodes along the curve that are connected by line segments. We then move these nodes according to the velocities \(\boldsymbol{v}\) by solving the system of ODEs: \[\begin{aligned} \frac{d\boldsymbol{x}^{(i)}}{dt} = \boldsymbol{v}(\boldsymbol{x}^{(i)},t),\quad \boldsymbol{x}^{(i)}(0) = \boldsymbol{x}^{(i)}_0, \end{aligned}\] where \(\boldsymbol{x}^{(i)}\) contains the coordinates of node \(i\), \(\boldsymbol{v}\) is the velocity function, and \(\boldsymbol{x}^{(i)}_0\) is the initial node location. This system can be solved accurately using explicit time integration schemes, e.g. forward Euler or Runge-Kutta methods.
When the velocity is given by \(F\boldsymbol{n}\), we have to evaluate \(\boldsymbol{n}\) at each node. We can approximate the tangent vector by central difference approximations involving the neighboring nodes, e.g. \[\begin{aligned} \frac{d\boldsymbol{x}^{(i)}}{ds}\approx \frac{\boldsymbol{x}^{(i+1)}-\boldsymbol{x}^{(i-1)}}{2\Delta s} \end{aligned}\] (assuming equal distance \(\Delta s\) between the nodes), and expressing the normal in terms of the tangent and normalizing. Similar approximations can be used to compute other geometric variables such as the curvature.
While this explicit scheme might be sufficient for small deformations of the initial interface, it has several drawbacks for general motions:
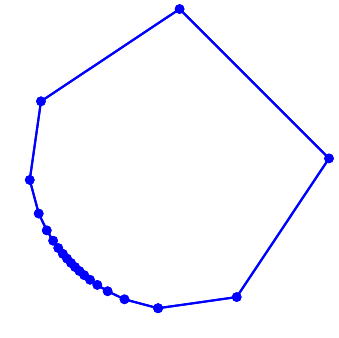
During the evolution, the nodes become unevenly distributed and the numerical representation of the curve gets inaccurate (see Figure 2, left). By inserting and removing nodes we can improve the representation, but this introduces errors.
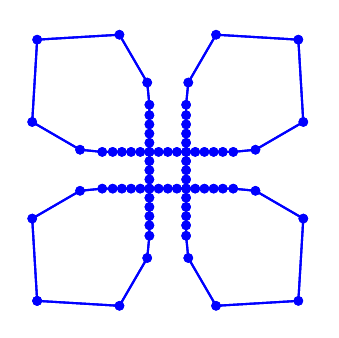
Around sharp corners, the scheme will not produce the desired “entropy solution”, but will generate an incorrect “shadowtail solution” (Figure 2, center).
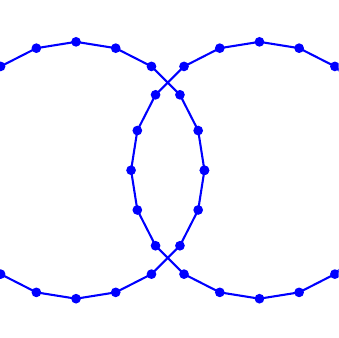
Topological changes, such as merging curves, require special treatment (Figure 2, right).
For curvature dependent speed functions \(F(\kappa)\), the scheme is sensitive to small perturbation which leads to instabilities unless the time steps are very small.
Node distribution
Sharp corners
Topology changes
Implicit Geometries
In the level set method, the interface is represented implicitly by the zero level set of a function, \(\phi(\boldsymbol{x})=0\). Note that \(\phi\) is defined for all \(\boldsymbol{x}\), not just the ones on the boundary. To represent \(\phi\) in a finite form on a computer, we discretize using a background mesh. A common choice is a simple Cartesian grid, but quadtrees or octrees can be used for higher efficiency. An example of a discretized implicit function is shown in Figure 3.
The actual interface can be extracted from bilinear interpolation in each grid cell, but the main philosophy of the level set method is that the interface should only be accessed implicitly by operating on \(\phi\). Exception to this are for plotting purposes, and possibly for the reinitialization (see below).
A special case of implicit representation is the signed distance function. It has the property that \(|\nabla\phi|=1\), with different signs at the two sides of the interface. Also, \(|\phi(\boldsymbol{x})|\) gives the (shortest) distance from \(\boldsymbol{x}\) to the boundary \(\phi=0\). The level set method does not require \(\phi\) to be a distance function, but the numerical approximations are inaccurate if \(\phi\) has large variations in the gradient. We therefore try to keep \(\phi\) close to a signed distance function, by frequent reinitializations (see below).
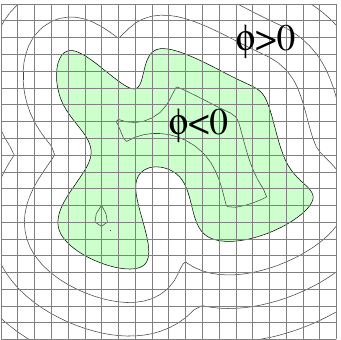
Geometric variables can be computed from \(\phi\) without extraction of the interface. The normal vector is given by \[\begin{aligned} \label{normal} \boldsymbol{n}=\frac{\nabla\phi}{|\nabla\phi|} \end{aligned}\] (since \(\phi\) is constant at a level set, \(\nabla\phi\) points in the normal direction). The curvature of a curve in two dimensions is \[\begin{aligned} \kappa=\nabla\cdot \frac{\nabla \phi}{|\nabla \phi|} = \frac{\phi_{xx}\phi_y^2-2\phi_y\phi_x\phi_{xy}+\phi_{yy}\phi_x^2}{(\phi_x^2+\phi_y^2)^{3/2}}. \end{aligned}\] In three dimensions, we compute the mean curvature \[\begin{aligned} \kappa_M=\nabla\cdot \frac{\nabla \phi}{|\nabla \phi|} = \frac {\left\{ \begin{array}{c} (\phi_{yy}+\phi_{zz})\phi_x^2+(\phi_{xx}+\phi_{zz})\phi_y^2+(\phi_xx+\phi_yy)\phi_z^2 \\ -2\phi_x\phi_y\phi_{xy}-2\phi_x\phi_z\phi_{xz}-2\phi_y\phi_z\phi_{yz} \end{array} \right\}} {(\phi_x^2+\phi_y^2+\phi_z^2)^{3/2}} \end{aligned}\] and the Gaussian curvature \[\begin{aligned} \kappa_G= \frac {\left\{ \begin{array}{c} \phi_x^2(\phi_{yy}\phi_{zz}-\phi_{yz}^2)+\phi_y^2(\phi_{xx}\phi_{zz}-\phi_{xz}^2) +\phi_z^2(\phi_{xx}\phi_{yy}-\phi_{xy}^2) \\ +2\small[\phi_x\phi_y(\phi_{xz}\phi_{yz}-\phi_{xy}\phi_{zz})+ \phi_y\phi_z(\phi_{xy}\phi_{xz}-\phi_{yz}\phi_{xx}) \\ + \phi_x\phi_z(\phi_{xy}\phi_{yz}-\phi_{xz}\phi_{yy}) \small] \end{array} \right\}} {(\phi_x^2+\phi_y^2+\phi_z^2)^2}. \end{aligned}\] From these the principal curvatures can be obtained as \(\kappa_M\pm \sqrt{\kappa_M^2-\kappa_G}\).
Using \(\phi\), we can also write different expressions for the two regions \(\phi<0\), and \(\phi>0\). For example, the density \[\begin{aligned} \rho(\boldsymbol{x}) = \rho_1 + (\rho_2-\rho_1)\theta(\phi(\boldsymbol{x})) \end{aligned}\] takes the value \(\rho_1\) for \(\phi<0\) and \(\rho_2\) for \(\phi>0\). On a discrete grid, the Heaviside function \(\theta(\boldsymbol{x})\) has to be approximated numerically for example by smoothing.
The Level Set Equation
Using the implicit representation \(\phi\), we can propagate the zero level set by the velocity field \(\boldsymbol{v}\) by solving the convection equation (we actually propagate all the level sets, not just \(\phi=0\)): \[\begin{aligned} \label{convection} \phi_t + \boldsymbol{v}\cdot \nabla\phi = 0. \end{aligned}\] For motion in the normal direction, we use ([normal]) and write \(\boldsymbol{v}=F\boldsymbol{n}=F\,\nabla\phi/|\nabla\phi|\). Insert in ([convection]) and use \(\nabla\phi\cdot\nabla\phi=|\nabla\phi|^2\) to obtain the Level Set Equation \[\begin{aligned} \label{levelsetequation} \phi_t+F|\nabla\phi|=0. \end{aligned}\]
Discretization
The convection equation ([convection]) can be solved numerically using first order upwinding. For the level set equation ([levelsetequation]), with use the following first order finite difference approximation: \[\begin{aligned} \label{eq:cartesian} \phi_{ijk}^{n+1}\ &= \phi_{ijk}^n - \Delta t \left( \max(F,0)\nabla^{+}_{ijk} + \min(F,0)\nabla^{-}_{ijk} \right), \end{aligned}\] where \[\begin{aligned} \label{eq:nablaplus} \nabla^{+}_{ijk} = \big[ & \max(D^{-x}\phi_{ijk}^n,0)^2+ \min(D^{+x}\phi_{ijk}^n,0)^2 + \nonumber \\ & \max(D^{-y}\phi_{ijk}^n,0)^2+ \min(D^{+y}\phi_{ijk}^n,0)^2 + \nonumber \\ & \max(D^{-z}\phi_{ijk}^n,0)^2+ \min(D^{+z}\phi_{ijk}^n,0)^2 \big] ^{1/2}, \end{aligned}\] \[\begin{aligned} \label{eq:nablaminus} \nabla^{-}_{ijk} = \big[ & \min(D^{-x}\phi_{ijk}^n,0)^2+ \max(D^{+x}\phi_{ijk}^n,0)^2 + \nonumber \\ & \min(D^{-y}\phi_{ijk}^n,0)^2+ \max(D^{+y}\phi_{ijk}^n,0)^2 + \nonumber \\ & \min(D^{-z}\phi_{ijk}^n,0)^2+ \max(D^{+z}\phi_{ijk}^n,0)^2 \big] ^{1/2}. \end{aligned}\] Here, \(D^{-x}\) is the backward difference operator in the \(x\)-direction, \(D^{+x}\) the forward difference operator, etc. For the curvature dependent part of \(F\), we use central difference approximations instead of ([eq:cartesian]). For further details and higher order schemes, see .
Reinitialization
After evolving \(\phi\) under a general speed function \(F\), it generally does not remain a signed distance function. We can reinitialize \(\phi\) by finding (a new) \(\phi\) with the same zero level set but with \(|\nabla\phi|=1\). Sussman et al proposed integrating the reinitialization equation \[\begin{aligned} \phi_t + \mathrm{sign}(\phi) ( |\nabla \phi| - 1 ) = 0 \end{aligned}\] for a short period of time. This equation can be discretized in a similar way as the level set equation, and the discontinuous sign function is smoothed over a few grid cells.
Another option is to explicitly update the nodes close the boundary, by for example extracting the curve segments and computing the distances to the grid nodes. For the remaining nodes, we can use the efficient fast marching method (see below).
The Boundary Value Formulation
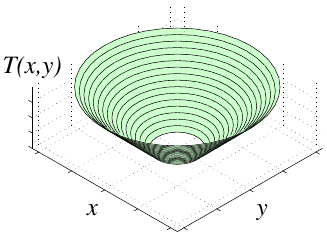
The level set equation ([levelsetequation]) is an initial value problem, where we track the zero level set \(\phi=0\) in time and ignore \(\phi\) away from the interface. If the speed function \(F>0\), we can alternatively formulate the evolution by an arrival function \(T\), with \(T(\boldsymbol{x})\) giving the time for the interface to reach \(\boldsymbol{x}\) from its initial location \(\Gamma\) (Figure 4). From the fact that time * rate = distance we can derive the boundary value problem known as the Eikonal equation: \[\begin{aligned} \label{eikonal} |\nabla T|F = 1, \quad T=0\text{ on }\Gamma. \end{aligned}\] An important special case is \(F=1\), when ([eikonal]) can be used to compute distance functions for the boundary \(\Gamma\).
The Fast Marching Methods
We can discretize the Eikonal equation ([eikonal]) using the same scheme as for the level set equation, to obtain the nonlinear algebraic system of equations \[\begin{aligned} \left[ \begin{array}{r} \max(D_{ijk}^{-x}T,0)^2+\min(D_{ijk}^{+x}T,0)^2 \\ +\max(D_{ijk}^{-y}T,0)^2+\min(D_{ijk}^{+y}T,0)^2 \\ +\max(D_{ijk}^{-z}T,0)^2+\min(D_{ijk}^{+z}T,0)^2 \\ \end{array} \right]^{1/2} = \frac{1}{F_{ijk}}. \end{aligned}\] Another possibility is the scheme \[\begin{aligned} \label{fmmdisc} \left[ \begin{array}{r} \max(D_{ijk}^{-x}T,-D_{ijk}^{+x}T,0)^2 \\ +\max(D_{ijk}^{-y}T,-D_{ijk}^{+y}T,0)^2 \\ +\max(D_{ijk}^{-z}T,-D_{ijk}^{+z}T,0)^2 \\ \end{array} \right]^{1/2} = \frac{1}{F_{ijk}} \end{aligned}\] which is slightly simpler because we choose either the forward or the backward difference along each dimensions (never both).
For efficient solution of ([fmmdisc]), we observe that front propagates outward from \(\Gamma\) and that nodes with higher value of \(T\) will never affect nodes with smaller values. This is the idea behind the Fast Marching Method (Sethian , see also Tsitsiklis ). The given boundary values are considered “known values”, and the nodes neighboring these can be updated by ([fmmdisc]) and inserted into a priority queue. The node with smallest unknown value can then by removed and marked as “known”, since it will not be affected by the other unknown values. Its neighbors are then updated by ([fmmdisc]) and inserted into the queue. This is repeated until all node values are “known”, and with a priority queue based on heaps the total computation requires \(\mathcal{O}(n\log n)\) operations for \(n\) nodes.