12. Computational Geometry#
How does a GPS navigate a complex network of streets? How does a video game render a 3D world in real-time? How does a robot map its environment to avoid obstacles? The answer to all these questions lies in computational geometry, a beautiful combination of classic geometry and computer science.
Computational geometry is about designing algorithms and data structures to solve problems involving geometric objects. It teaches computers how to “reason” about space, shape, and position. The field is often split into two main branches:
12.1. 1. Combinatorial Computational Geometry#
This branch is the “logic” side of the field. It deals with problems involving discrete geometric objects like points, lines, polygons, and polyhedra. The focus is on the properties and relationships between these fundamental shapes. Most of the problems we’ll cover in this chapter fall in this category:
Convex Hull: Imagine stretching a rubber band around a set of nails on a board. What shape does it make? This is the convex hull, the smallest convex polygon that encloses all the points.
Line Segment Intersection: Given a collection of lines, how can we efficiently find all the points where they cross? This is crucial for detecting collisions in simulations and games.
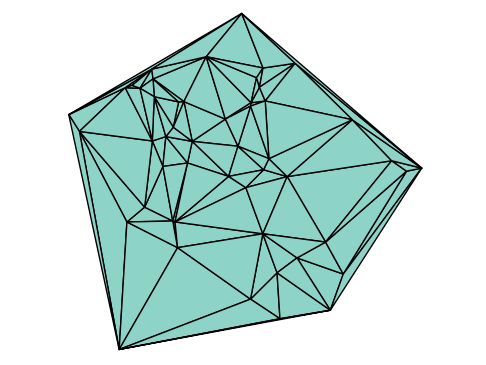
Polygon Triangulation: How can we divide any polygon into a set of non-overlapping triangles? This is a foundational step for rendering graphics and for many engineering simulations.
Point in Polygon: A classic problem: given a point and a complex polygon, is the point inside or outside? This is used everywhere from geographic information systems (GIS) to video game physics.
12.2. 2. Numerical Computational Geometry#
This branch is the “modeling” side, closely related to Computer-Aided Design (CAD) and manufacturing. It focuses on representing and manipulating smooth curves and surfaces, often using mathematical forms like Bézier curves or splines. This is essential for designing everything from cars and airplanes to intricate movie characters and industrial parts. Key problems include creating efficient digital representations of complex shapes and calculating their interactions, like finding the intersection between two curved surfaces.