17.3. Application: Graphs using sparse matrices#
While we used adjacency lists to store our graphs previously, it is also possible to use adjancency matrices. For an unweighted graph with vertices \(V,E\), the adjancency matrix \(A\) is of size \(|V|\)-by-\(|V|\), and entries \(A_{ij}=1\) if the graph has an edge from vertex \(i\) to vertex \(j\), otherwise zero.
These can be stored conveniently using Julia’s sparse matrices. Note that the actual implementation using the CSC format is quite similar to the adjancency list. However, insertion of new edges (and vertices) is still very expensive.
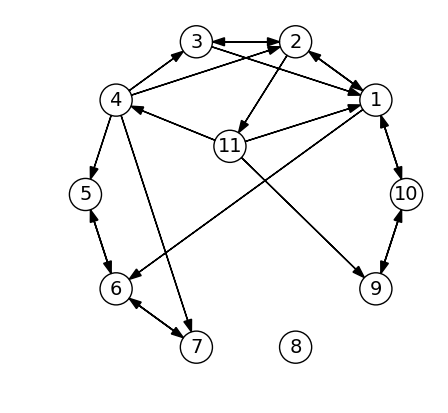
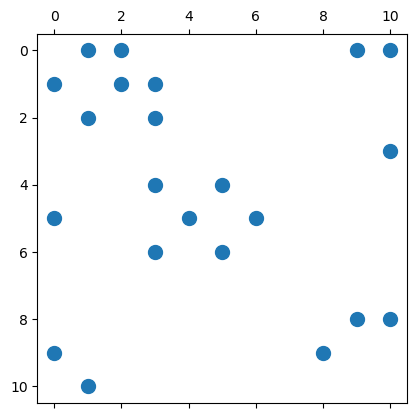
As an example, we create the same graph as used in the section on graph algorithms. Since the CSC format stores non-zeros column-by-column, we use the transpose \(A^T\) instead of \(A\) itself. This makes it faster to find all the neighbors of a vertex, by finding the non-zeros in a column (instead of a row).
using PyPlot, SparseArrays, LinearAlgebra # Packages used
rows = [1,1,1,2,2,2,3,3,4,4,4,4,5,6,6,7,9,10,10,11,11,11]
cols = [2,10,6,3,1,11,1,2,5,3,2,7,6,7,5,6,10,1,9,1,4,9]
AT = sparse(cols, rows, 1, 11, 11) # Use transpose, better for finding neighbors
spy(AT, marker=".", markersize=20);
To illustrate how to use this adjacency matrix, we repeat the DFS algorithm.
The main operation is the loop over all neighbors of ivertex, which are given
by the locations of the non-zeros in a column: findall(AT[:,ivertex]).
function sparse_dfs(AT, start)
visited = falses(size(AT,1))
function visit(ivertex)
visited[ivertex] = true
println("Visiting vertex #$ivertex")
for nb in findall(AT[:,ivertex] .!= 0)
if !visited[nb]
visit(nb)
end
end
end
visit(start)
return nothing
end
sparse_dfs (generic function with 1 method)
sparse_dfs(AT, 1)
Visiting vertex #1
Visiting vertex #2
Visiting vertex #3
Visiting vertex #11
Visiting vertex #4
Visiting vertex #5
Visiting vertex #6
Visiting vertex #7
Visiting vertex #9
Visiting vertex #10

